Statistics and Modelling

Meenakshi Kushwaha

1st September, 2022

Packages for today

library(gapminder) # dataset
library(tidyverse) # data wrangling
library(here) # file path
library(gtsummary) # summary statistics tables
library(flextable) # saving tables as word file

Today we will cover (a lot)

• Summary statistics
• Linear Regression models
• Handling multiple models
• Machine Learning terminology (very briefly)

Presenting Summary Statistics

Simple table in R

gapminder %>% 
  filter(country == "India",
         year > 1980) %>% 
  select(year, pop, lifeExp ) %>% 
  knitr::kable() # print in table format

year	pop	lifeExp
1982	708000000	56.596
1987	788000000	58.553
1992	872000000	60.223
1997	959000000	61.765
2002	1034172547	62.879
2007	1110396331	64.698

Summary Statistics

Generate summary statistics by continent for gapminder dataset

gapminder %>% 
  select(-country) %>% # drop country variable
  tbl_summary()

Characteristic	N = 1,7041
continent
Africa	624 (37%)
Americas	300 (18%)
Asia	396 (23%)
Europe	360 (21%)
Oceania	24 (1.4%)
year	1,980 (1,966, 1,993)
lifeExp	61 (48, 71)
pop	7,023,596 (2,793,664, 19,585,222)
gdpPercap	3,532 (1,202, 9,325)
1 n (%); Median (IQR)

Customizing your table

gapminder %>% 
  select(-country) %>% # drop country variable
  tbl_summary(include = -year)

Characteristic	N = 1,7041
continent
Africa	624 (37%)
Americas	300 (18%)
Asia	396 (23%)
Europe	360 (21%)
Oceania	24 (1.4%)
lifeExp	61 (48, 71)
pop	7,023,596 (2,793,664, 19,585,222)
gdpPercap	3,532 (1,202, 9,325)
1 n (%); Median (IQR)

Customizing your table

gapminder %>% 
  select(-country) %>% # drop country variable
  tbl_summary(include = c(continent, lifeExp, gdpPercap))

Characteristic	N = 1,7041
continent
Africa	624 (37%)
Americas	300 (18%)
Asia	396 (23%)
Europe	360 (21%)
Oceania	24 (1.4%)
lifeExp	61 (48, 71)
gdpPercap	3,532 (1,202, 9,325)
1 n (%); Median (IQR)

Customizing your table

gapminder %>% 
  select(-country, - year) %>% # drop country and year variable
  tbl_summary() %>% 
  bold_labels()

Characteristic	N = 1,7041
continent
Africa	624 (37%)
Americas	300 (18%)
Asia	396 (23%)
Europe	360 (21%)
Oceania	24 (1.4%)
lifeExp	61 (48, 71)
pop	7,023,596 (2,793,664, 19,585,222)
gdpPercap	3,532 (1,202, 9,325)
1 n (%); Median (IQR)

See tutorial for more options

Saving your summary table

• Save as image, RTF, LaTeX, and Word file
• Embed in Rmarkdown output . . .

Save your table as .docx file

gapminder %>% 
  select(-country, - year) %>% # drop country and year variable
  tbl_summary() %>% 
  as_flex_table() %>% # save table as Word file 
  save_as_docx(path = here("myfile.docx")) 

Syntax for other formats

Demo

Modelling

A simple linear model in R

What is the relationship between Life Expectancy and Population

lm(lifeExp ~ pop, data = gapminder)

is the same as

gapminder %>% 
  lm(lifeExp ~ pop, data = .)

Linear regression in R

lm (outcome ~ exp var 1 + exp var 2 +...., data = <your_df>)

is the same as

your_df %>% lm(outcome ~ exp var 1 + exp var 2 +...., data =.)

The + here means include and not addtion

Your first linear model

gapminder %>% 
  lm(lifeExp ~ year, data = .) 

Call:
lm(formula = lifeExp ~ year, data = .)

Coefficients:
(Intercept)         year  
  -585.6522       0.3259  

Your first linear model

Now, we will assign the model to an object to extract more information

my_model <- gapminder %>% 
  lm(lifeExp ~ year, data = .) 

summary(my_model)

Call:
lm(formula = lifeExp ~ year, data = .)

Residuals:
    Min      1Q  Median      3Q     Max 
-39.949  -9.651   1.697  10.335  22.158 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -585.65219   32.31396  -18.12   <2e-16 ***
year           0.32590    0.01632   19.96   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 11.63 on 1702 degrees of freedom
Multiple R-squared:  0.1898,    Adjusted R-squared:  0.1893 
F-statistic: 398.6 on 1 and 1702 DF,  p-value: < 2.2e-16

Notice that this is the same summary function that you use with df. But depending on the input, it will give diff output.

Testing model assumptions

arg_model <- gapminder %>% 
  filter(country == "Argentina") %>% 
  lm(lifeExp ~ year, data = .)
plot(arg_model) # generates four diagnostic plots

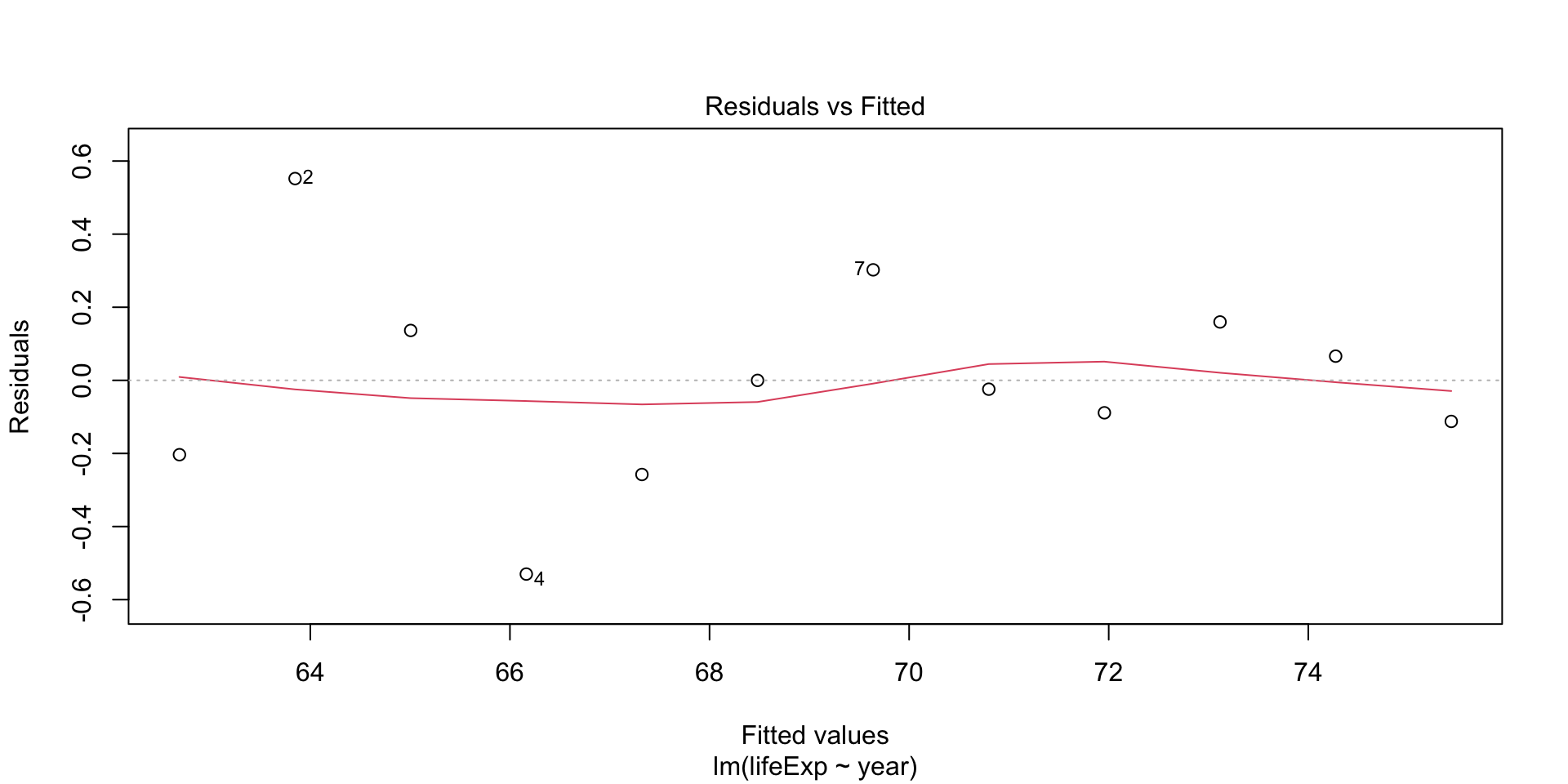
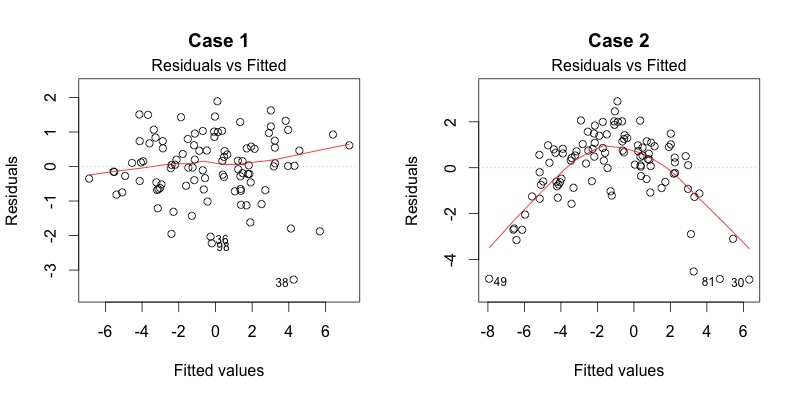
Plot diagnostics - residual vs fitted

Residuals should be equally spread around the horizontal line - any patterns indicate non-linear relationsihp

Source

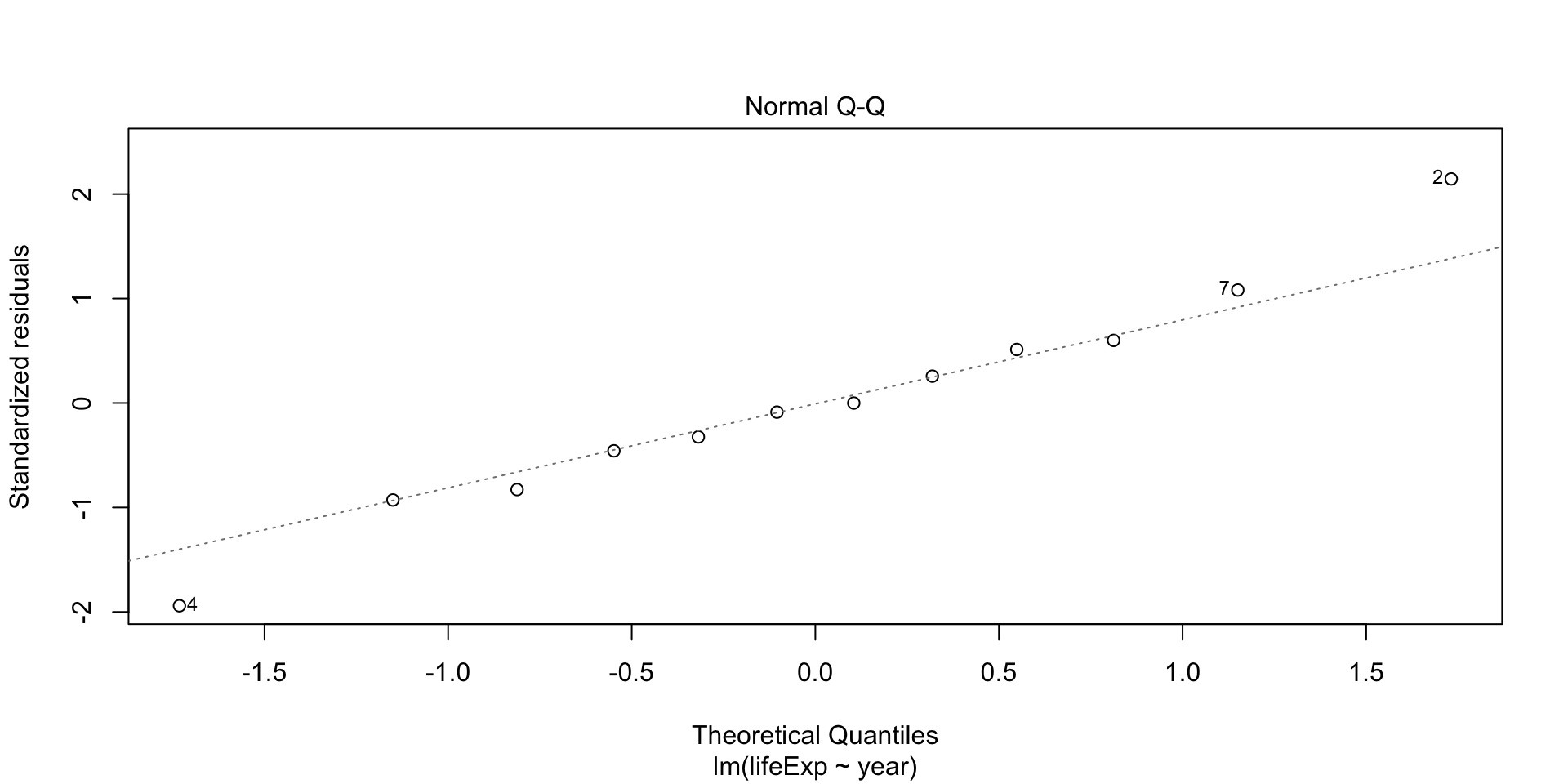
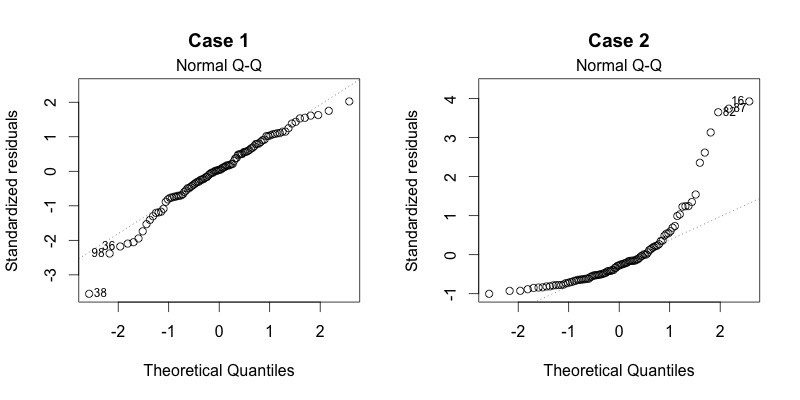
Plot diagnostics - Normal Q-Q

Residuals are normally distributed if dots fall on the straight line

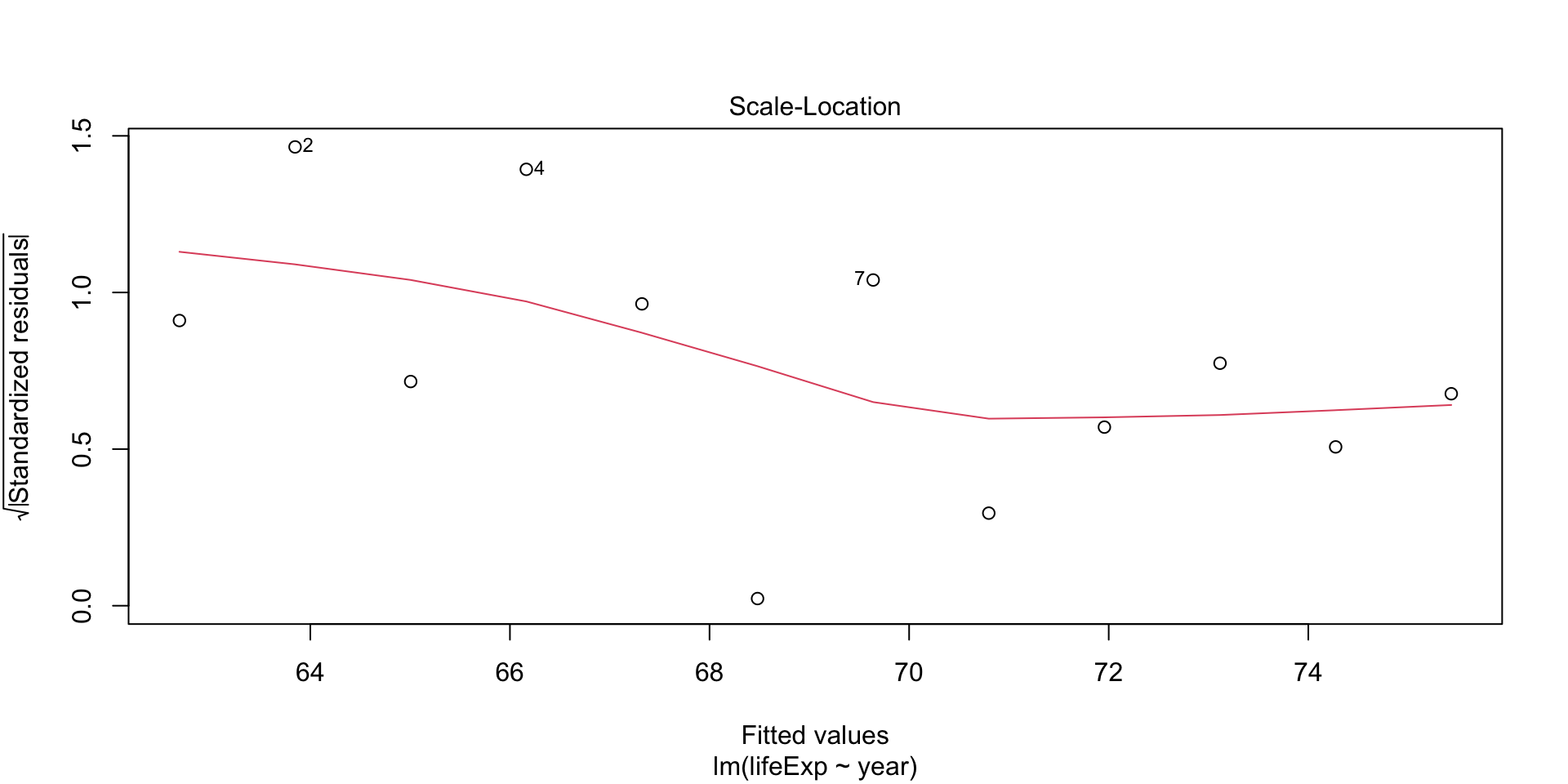
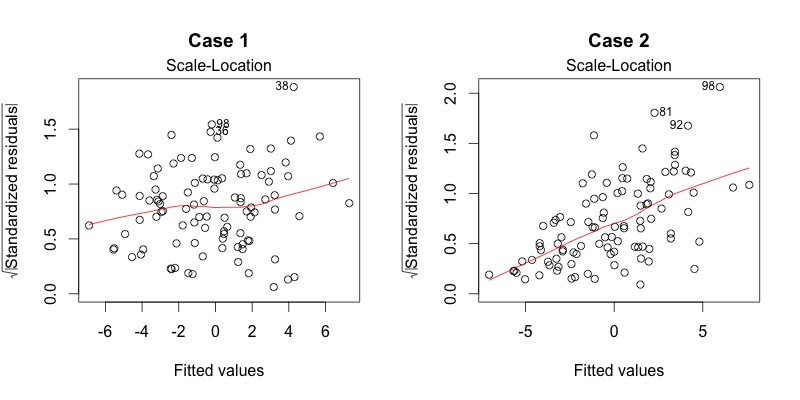
Plot diagnostics - Scale-location

This plot shows if residuals are spread equally along the range of predictors

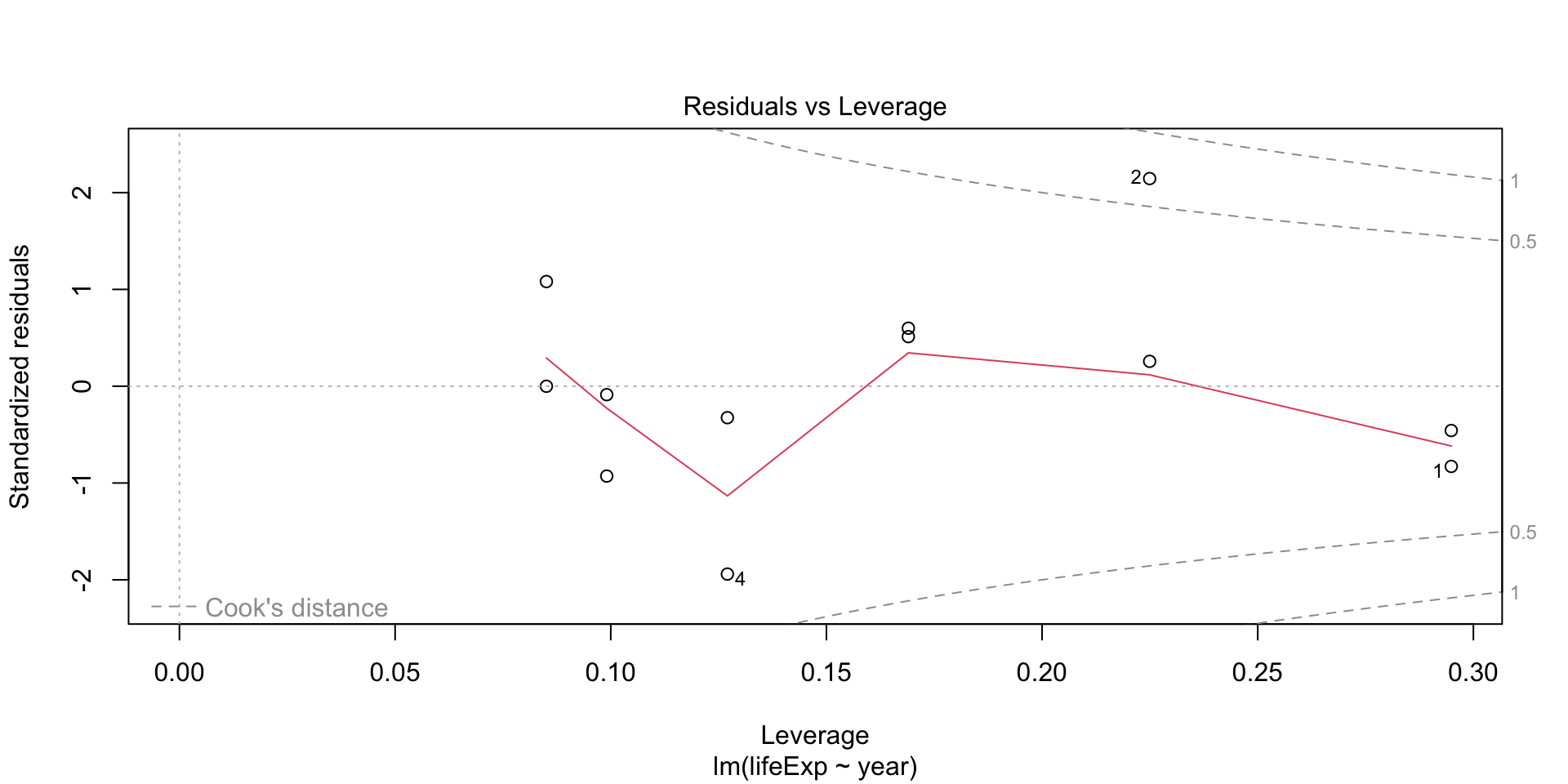
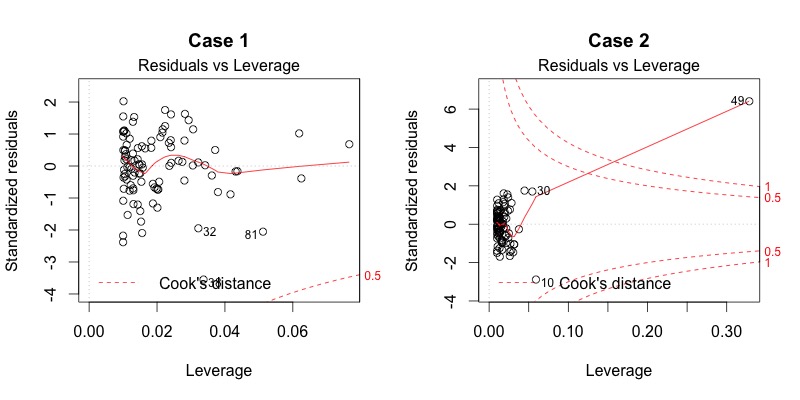
Plot diagnostics - Residuals vs Leverage

Are there influential points in the data

Demo

Multiple models

How does life expectancy change with time in each country

Global vs local trend

gapminder %>%
  ggplot(aes(x = year, y = lifeExp, group = country)) +
  geom_line(alpha = 1/3)

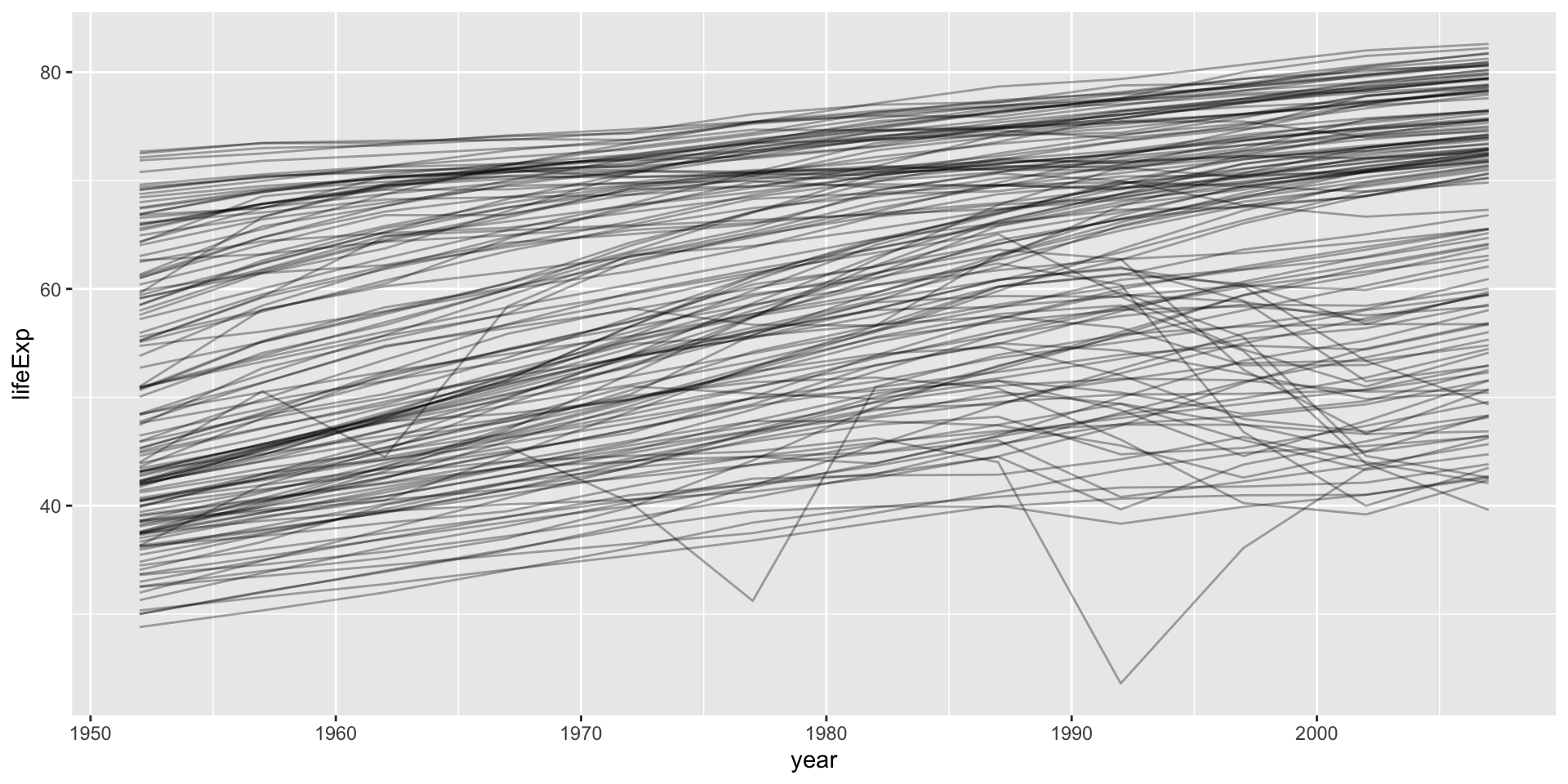
Keep related things together group_nest()

Nest by country

by_country <- gapminder %>% 
  mutate(year1950 = year - 1950) %>% 
  group_nest(continent, country)
head(by_country, 4)

# A tibble: 4 × 3
  continent country                data
  <fct>     <fct>    <list<tibble[,5]>>
1 Africa    Algeria            [12 × 5]
2 Africa    Angola             [12 × 5]
3 Africa    Benin              [12 × 5]
4 Africa    Botswana           [12 × 5]

• by default list column is named data
• year1950 for meaningful intercepts
• add continent to keep it along with country

One country example

• From original tibble
• From nested tibble

gapminder %>% 
  filter(country == "India") %>% 
  select(-country, -continent)

# A tibble: 12 × 4
    year lifeExp        pop gdpPercap
   <int>   <dbl>      <int>     <dbl>
 1  1952    37.4  372000000      547.
 2  1957    40.2  409000000      590.
 3  1962    43.6  454000000      658.
 4  1967    47.2  506000000      701.
 5  1972    50.7  567000000      724.
 6  1977    54.2  634000000      813.
 7  1982    56.6  708000000      856.
 8  1987    58.6  788000000      977.
 9  1992    60.2  872000000     1164.
10  1997    61.8  959000000     1459.
11  2002    62.9 1034172547     1747.
12  2007    64.7 1110396331     2452.

by_country %>% 
  filter(country == "India") %>% 
  unnest(data)

# A tibble: 12 × 7
   continent country  year lifeExp        pop gdpPercap year1950
   <fct>     <fct>   <int>   <dbl>      <int>     <dbl>    <dbl>
 1 Asia      India    1952    37.4  372000000      547.        2
 2 Asia      India    1957    40.2  409000000      590.        7
 3 Asia      India    1962    43.6  454000000      658.       12
 4 Asia      India    1967    47.2  506000000      701.       17
 5 Asia      India    1972    50.7  567000000      724.       22
 6 Asia      India    1977    54.2  634000000      813.       27
 7 Asia      India    1982    56.6  708000000      856.       32
 8 Asia      India    1987    58.6  788000000      977.       37
 9 Asia      India    1992    60.2  872000000     1164.       42
10 Asia      India    1997    61.8  959000000     1459.       47
11 Asia      India    2002    62.9 1034172547     1747.       52
12 Asia      India    2007    64.7 1110396331     2452.       57

Linear model per country

by_country_lm <- by_country %>% 
  mutate(model = map(data, ~lm(lifeExp ~ year1950, data = .)))# to each element of data column apply lm() function
by_country_lm

# A tibble: 142 × 4
   continent country                                data model 
   <fct>     <fct>                    <list<tibble[,5]>> <list>
 1 Africa    Algeria                            [12 × 5] <lm>  
 2 Africa    Angola                             [12 × 5] <lm>  
 3 Africa    Benin                              [12 × 5] <lm>  
 4 Africa    Botswana                           [12 × 5] <lm>  
 5 Africa    Burkina Faso                       [12 × 5] <lm>  
 6 Africa    Burundi                            [12 × 5] <lm>  
 7 Africa    Cameroon                           [12 × 5] <lm>  
 8 Africa    Central African Republic           [12 × 5] <lm>  
 9 Africa    Chad                               [12 × 5] <lm>  
10 Africa    Comoros                            [12 × 5] <lm>  
# … with 132 more rows

Quiz

1. How would you count how many rows are there per country?
2. Plot Life expectancy LifeExp VS Year for India

map practice

How many rows per country?

by_country_lm %>% 
  mutate(n = map_int(data, nrow)) %>% 
  select(country, n) %>% 
  head(4)

# A tibble: 4 × 2
  country      n
  <fct>    <int>
1 Algeria     12
2 Angola      12
3 Benin       12
4 Botswana    12

Do all countries have the same amount of data? Check if all have same # of rows?

by_country_lm %>% 
 mutate(n = map_int(data, nrow)) %>% 
  distinct(n)

# A tibble: 1 × 1
      n
  <int>
1    12

Plotting for one country

by_country_lm %>% 
  filter(country=="India") %>% 
  unnest(data) %>% 
  ggplot(aes(x = year1950, y = lifeExp)) +
  geom_line()

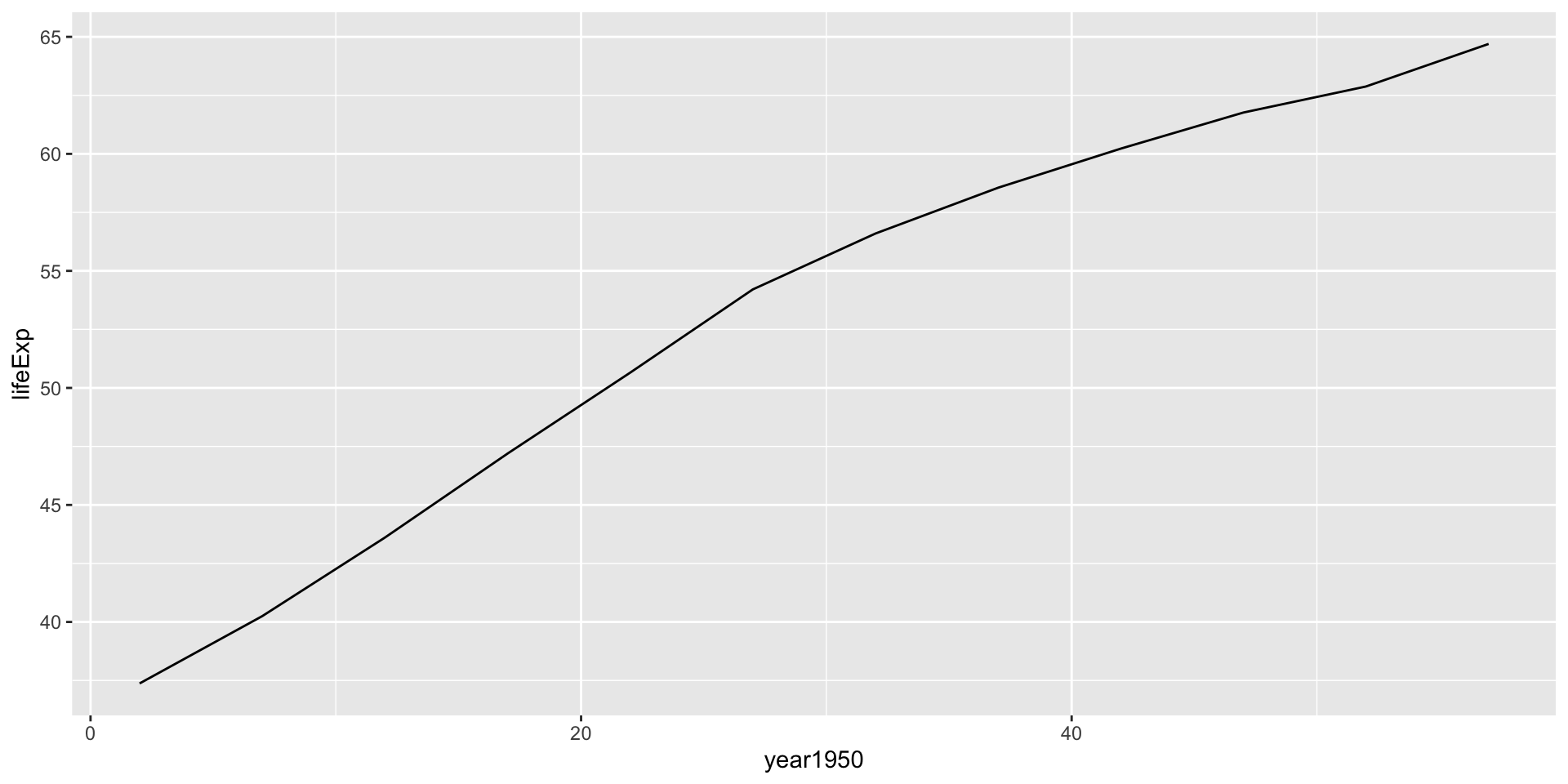
Linear model for India

by_country_lm%>% 
  filter(country == "India") %>% 
  pluck("model", 1) %>% 
  summary()

Call:
lm(formula = lifeExp ~ year1950, data = .)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.36441 -1.57472  0.04961  1.35537  2.30522 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 38.25911    0.98600   38.80 3.09e-12 ***
year1950     0.50532    0.02885   17.52 7.81e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.725 on 10 degrees of freedom
Multiple R-squared:  0.9684,    Adjusted R-squared:  0.9653 
F-statistic: 306.8 on 1 and 10 DF,  p-value: 7.813e-09

Linear model for Rwanda

by_country_lm%>% 
  filter(country == "Rwanda") %>% 
  pluck("model", 1) %>% 
  summary()

Call:
lm(formula = lifeExp ~ year1950, data = .)

Residuals:
    Min      1Q  Median      3Q     Max 
-17.310  -1.445   2.410   3.073   6.021 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 42.83361    3.74890  11.426 4.63e-07 ***
year1950    -0.04583    0.10969  -0.418    0.685    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.558 on 10 degrees of freedom
Multiple R-squared:  0.01716,   Adjusted R-squared:  -0.08112 
F-statistic: 0.1746 on 1 and 10 DF,  p-value: 0.6849

Verify by plotting for Rwanda

by_country_lm %>% 
  filter(country=="Rwanda") %>% 
  unnest(data) %>% 
  ggplot(aes(x = year1950, y = lifeExp)) +
  geom_line()

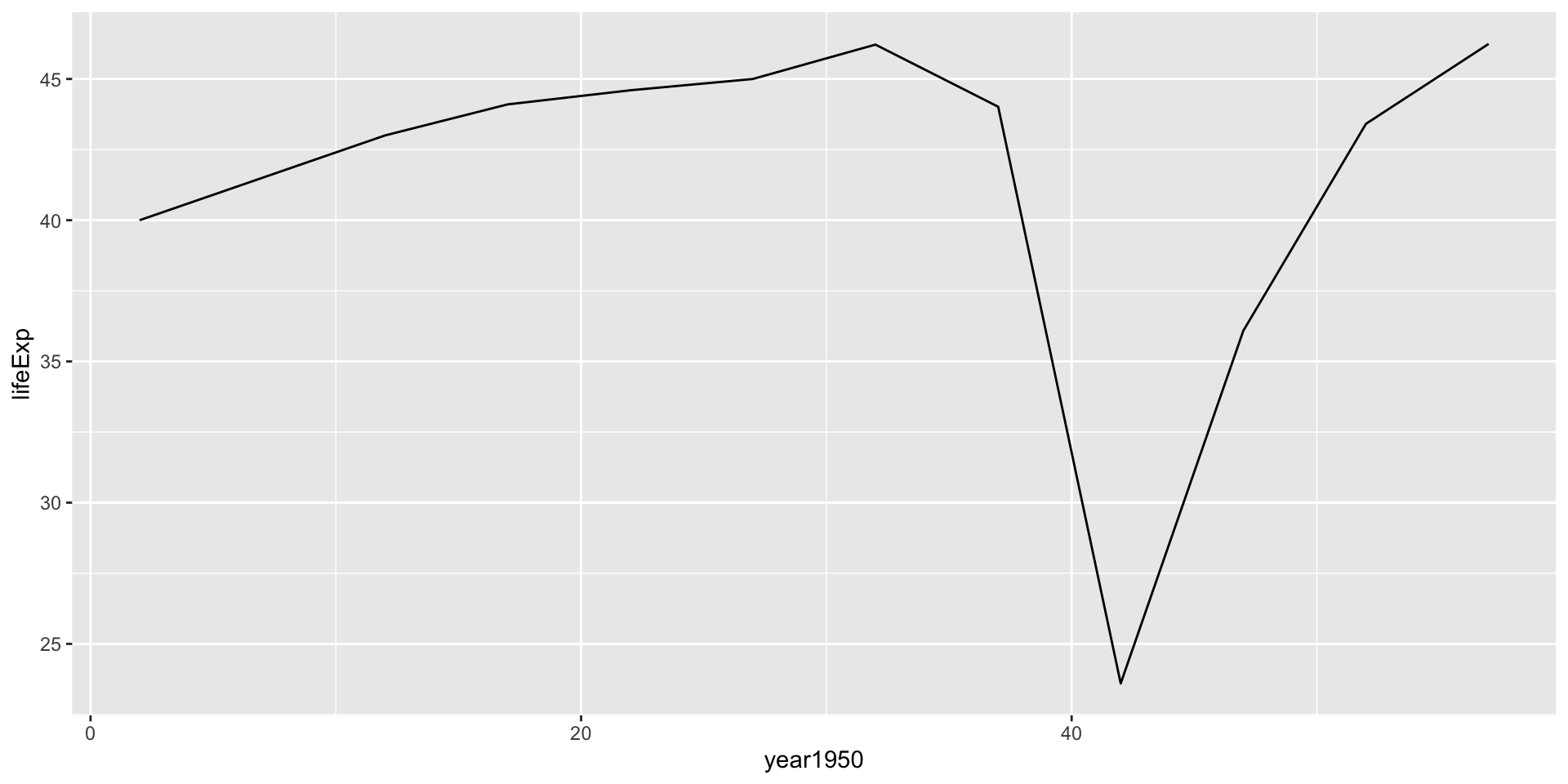
Cleaning model outputs using broom package

• tidy() summarizes information about model components
• glance() reports information about the entire model
• augment() adds informations about observations to a dataset

Lear more here

How doesbroom clean up model outputs

Source

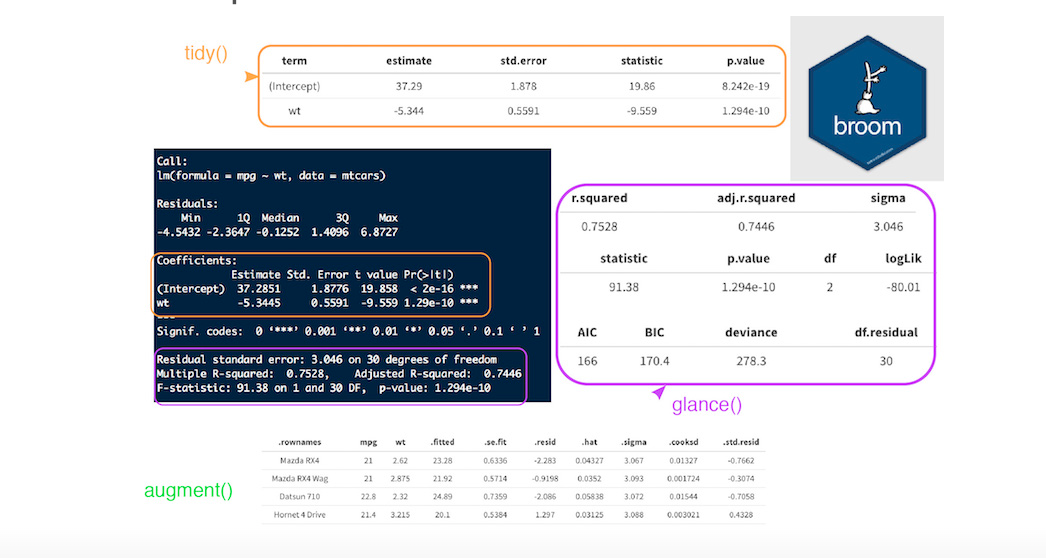
Tyding models

Extract from nested lists

library(broom)
gm_models <- by_country_lm %>% 
  mutate(glance= map(model, glance),
         tidy = map(model, tidy),
         augment = map(model, augment),
         rsq = map_dbl(glance, "r.squared"))

gm_models

# A tibble: 142 × 8
   continent country                data model glance   tidy     augment     rsq
   <fct>     <fct>              <list<t> <lis> <list>   <list>   <list>    <dbl>
 1 Africa    Algeria            [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.985 
 2 Africa    Angola             [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.888 
 3 Africa    Benin              [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.967 
 4 Africa    Botswana           [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.0340
 5 Africa    Burkina Faso       [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.919 
 6 Africa    Burundi            [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.766 
 7 Africa    Cameroon           [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.680 
 8 Africa    Central African R… [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.493 
 9 Africa    Chad               [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.872 
10 Africa    Comoros            [12 × 5] <lm>  <tibble> <tibble> <tibble> 0.997 
# … with 132 more rows

Do linear models fit all countries?

library(forcats) # working with factors
gm_models %>%
  ggplot(aes(x = rsq, 
             y = fct_reorder(country,
                             rsq))) +
  geom_point(aes(colour = continent), 
             alpha = 0.5) +
  theme_classic() +
  theme(axis.text.y = element_blank(), 
        axis.ticks.y = element_blank())+
  labs(x = "r square",
       y = "Country") 

Do linear models fit all countries?

Countries with non-linear trends

Focus on countries with low rsq

gm_models %>% 
  top_n(20, desc(rsq)) %>% # select rows by value
  unnest(data) %>%
  ggplot(aes(x = year, y = lifeExp)) +
  geom_line(aes(colour = continent)) +
  facet_wrap(~ country) +
  theme(axis.text.x = element_text(angle = 45,
                                   hjust = 1),
        legend.position = "bottom")

Countries with non-linear trends

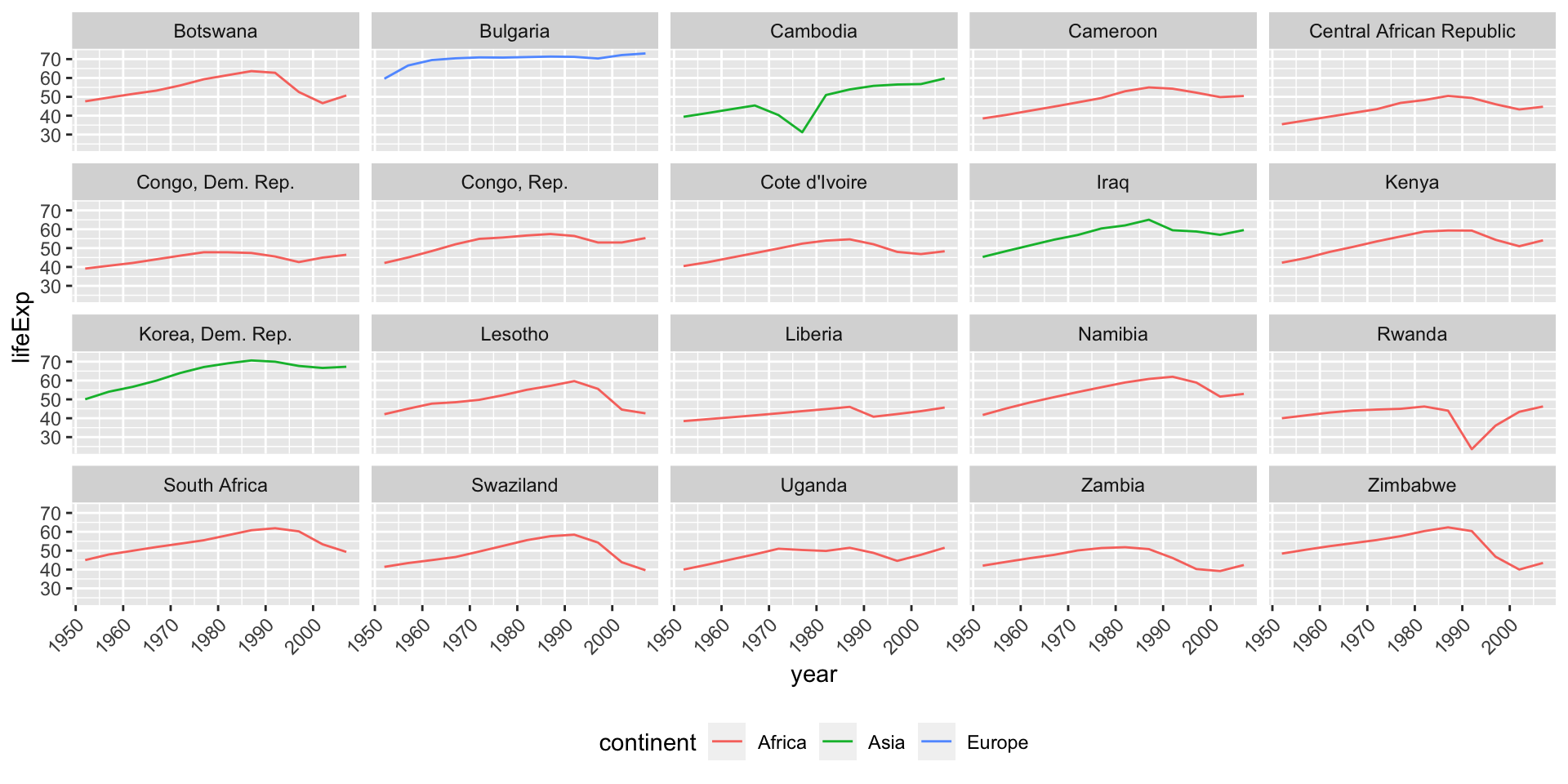
Countries with strong linear trends

Focus on countries with high rsq

gm_models %>% 
  top_n(20, rsq) %>%
  unnest(data) %>%
  ggplot(aes(x = year, y = lifeExp)) +
  geom_line(aes(colour = continent)) +
  facet_wrap(~ country) +
  theme(axis.text.x = element_text(angle = 45,
                                   hjust = 1),
        legend.position = "bottom")

Countries with strong linear trends

Interpreting the linear model

India, lifeExp~year1950

by_country_lm %>% 
  filter(country=="India") %>% 
  unnest(data) %>% 
  ggplot(aes(x = year1950, y = lifeExp)) +
  geom_line()

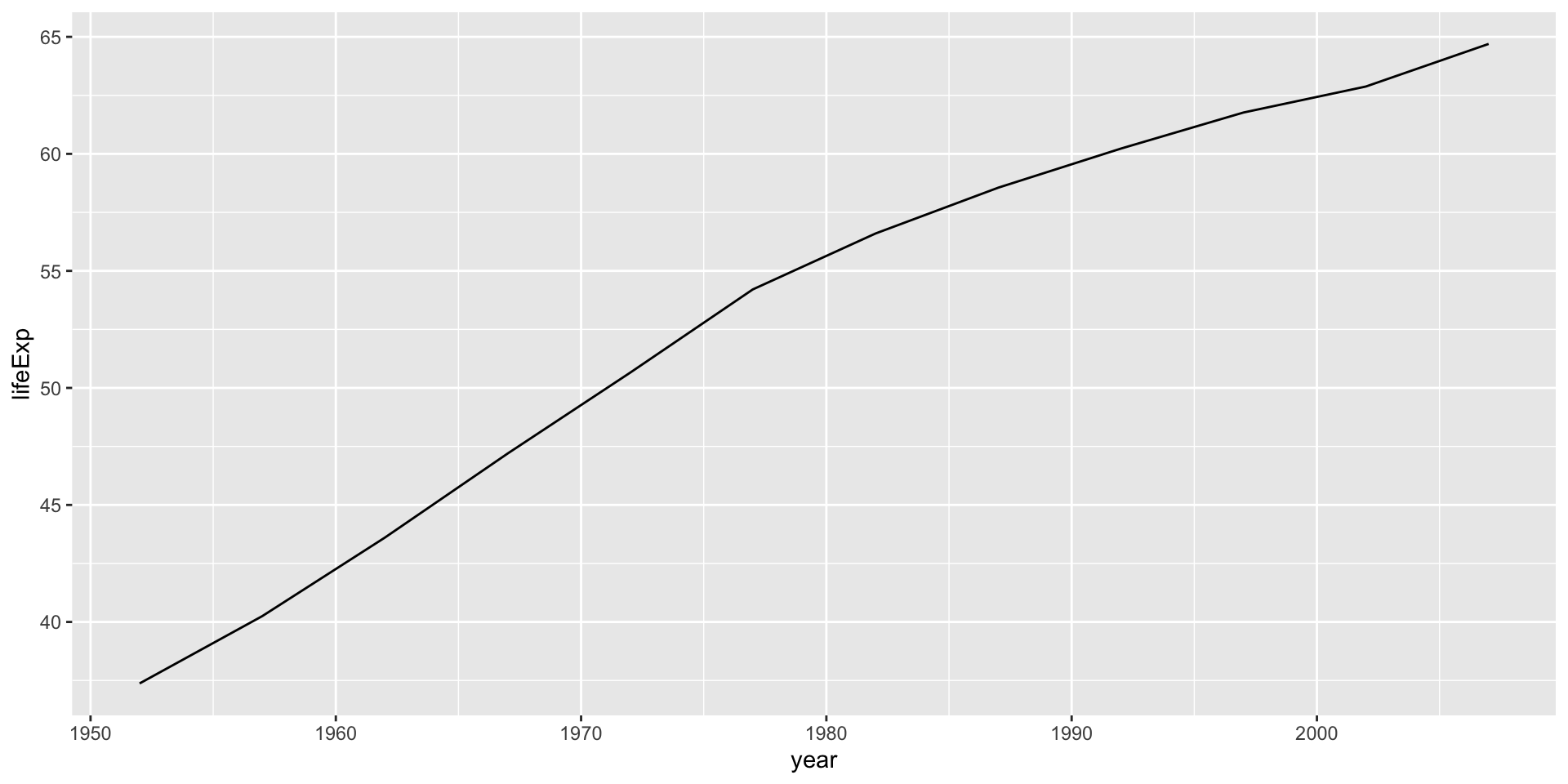
Interpreting the linear model

India, lifeExp~year

by_country_lm %>% 
  filter(country=="India") %>% 
  unnest(data) %>% 
  ggplot(aes(x = year, y = lifeExp)) +
  geom_line()

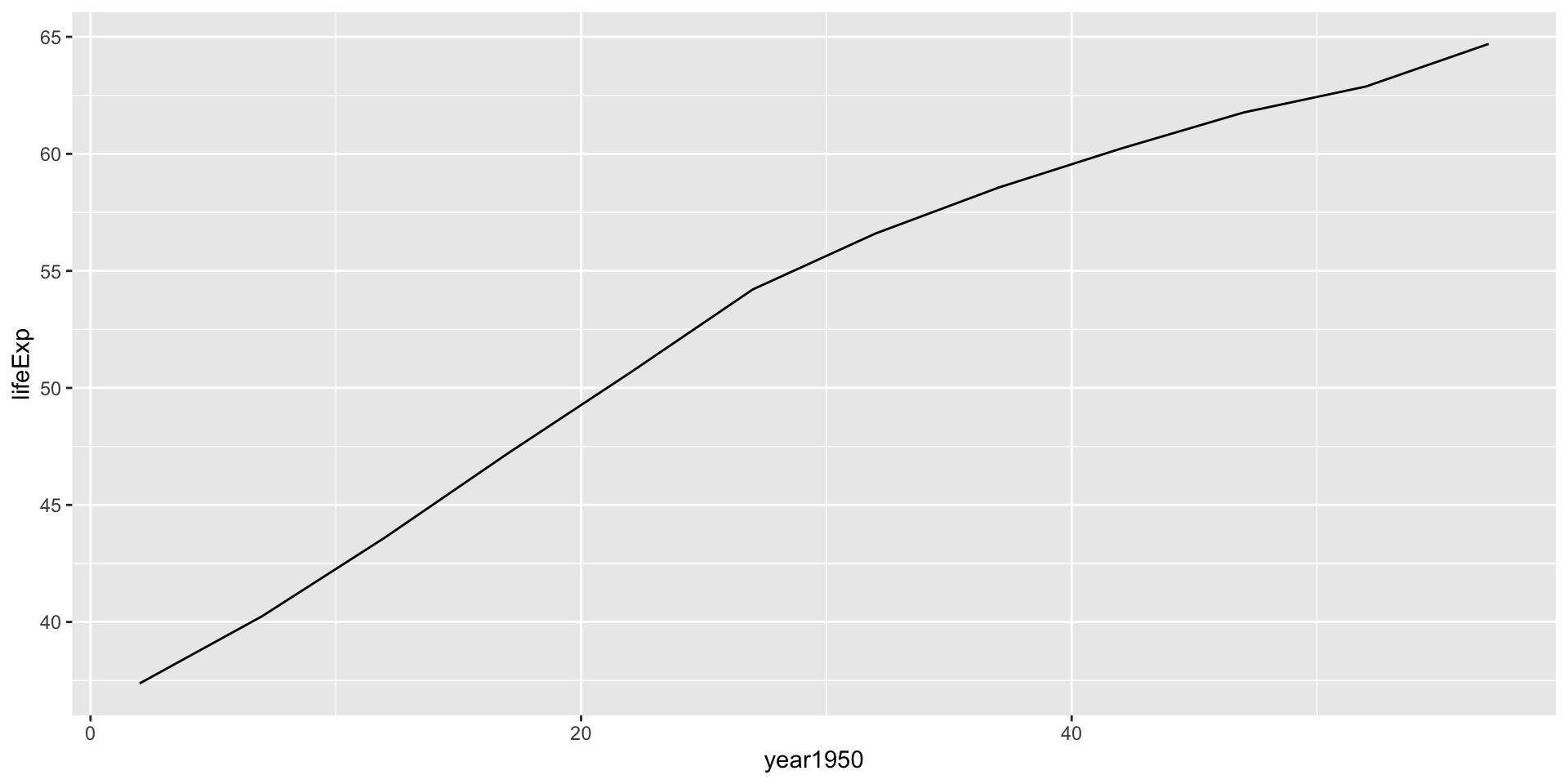
Visualizing all models

gm_models %>%
  unnest(tidy) %>%
  select(continent, country, rsq, term, estimate) %>%
  pivot_wider(names_from = term, values_from = estimate) %>%
  ggplot(aes(x = `(Intercept)`, y = year1950)) +
  geom_point(aes(colour = continent, size = rsq)) +
  geom_smooth(se = FALSE, method = "loess") +
  scale_size_area() + labs(x = "Life expectancy (1950)", y = "Yearly improvement")

Visualizing all models

Where does Linear regression fit in Machine Learning?

ML Cheatsheet

Resources

-Tutorial by A. Ginolhac

-R for Data Science Book - Modelling chapters